
Method of Construction of Index Number
1 Introduction:
Index number measures the relative change in the value of the variable with respect to time. For example, they are used to measure the change in the price of the commodity, income status of the people, the employment rate of the people, price hike, etc with respect to some base period. It is always expressed in percentage form for comparison, the index number for the base period is always equal to 100%.
1 Method of Construction of Index Number:
There are mainly two methods used in the construction of index numbers.
i) Unweighted Index Number:
ii) Weighted Index Number:
i) Unweighted Index Number: In this method, all the items are considered equally important i.e. it assumed that the weight of all items is the same. Under this method, we use the following two methods to obtain the index number.
a. Unweighted Aggregate /Simple Index Number:
b. Unweighted Average of Relative Method:
a) Unweighted Aggregate / Simple Index Number :
• Unweighted aggregate price index number for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
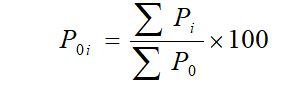
• Unweighted aggregate quantity index number for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
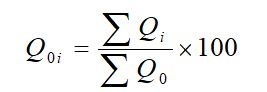
• Unweighted aggregate value index number for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
![]()
The notations have their usual meaning.
b) Unweighted average of relative method:
• Unweighted averages of the relative price index for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
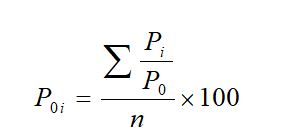
Where ‘n’ is the number of products or number of elements.
• Unweighted averages of relative quantity index for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
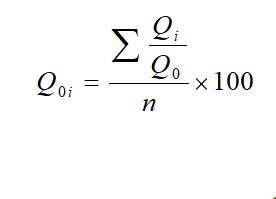
The notations have their usual meaning.
ii) Weighted Index Number: In this method, appropriate weights are assigned to the commodities according to their importance. Under this method, we use two methods to obtain the index number.
a. Weighted aggregate methods:
b. Weighted average of relative methods:
a. Weighted aggregate methods:
Under this method, we use Laspeyres and Paasche index number.
i) Laspeyres index number:
a. Laspeyres price index number: Laspeyres index number takes the base period quantity (Q0) as a weighting factor; it is obtained by using the following relation.
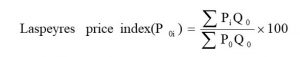
b. Laspeyres quantity index number: Laspeyres quantity index number takes the base period price (P0) as a weighting factor; it is obtained by using the following relation
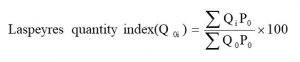
ii) Paasche index number:
a. The Paasche price index number takes the current period quantity (Qi) as a weighting factor and it is obtained by using the following relation.
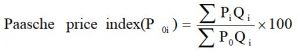
b. Paasche quantity index number: Paasche quantity index number takes the current period price (Pi) as a weighting factor and it is obtained by using the following relation
![]()
Note:
• Fisher index number: Fisher index number is the geometric mean of the Laspeyres and Paasche index number. Mathematically,
![]()
Where
L.P.I.N= Laspeyres Price Index Number
P.P.I.N= Paasche Price Index Number.
Note:
• Fixed weight aggregative method: In this method, weight is assigned from any period instead of base and current period.
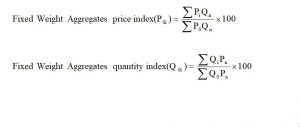
b. Weighted Average of Relative Method:
• Weighted average of relative price index number: The weighted average of the relative price index for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
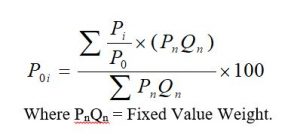
Note:
If the base period is used for the weight (value weight) then replace PnQn by P0Q0 in the above relation.
If the current period is used for the weight (value weight) then replace PnQn by PiQi in the above relation.
• Weighted average of relative quantity index number: The weighted average of relative quantity index for the current period ‘i’ compared to base period ‘0’ is obtained by using the following relation.
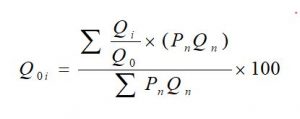
Where PnQn = Fixed Value Weight.
Note:
If the base period is used for the weight (value weight) then replace PnQn by P0Q0 in the above relation.
If the current period is used for the weight (value weight) then replace PnQn by PiQi in the above relation.
2 Cost of Living /Consumer Price Index Number:
Cost of Living /Consumer Price Index Number measures the average change in the cost of maintaining a living standard of the people in the current period compared to the base period (reference period) i.e. It measures the change in average retail price paid by a specific class of people to maintain their previous living standard in the current period. Two methods are used to obtain the cost of living index number.
• Aggregate expenditure method: in this method, the cost of living index number is obtained by using the following relation.
![]()
This is also known as the Laspeyres price index number.
• Family budget method: in this method, the cost of living index number is obtained by using the following relation.
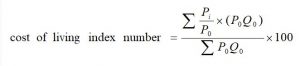
This formula can be written in the following form.
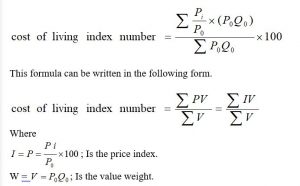
3 Uses of index numbers:
They are very useful in studying the change in the trend or tendency of a series over a period of time. With the help of index numbers, it is easy to find out the trend of exports, imports, the balance of payment, industrial production, price, national income, and a variety of other phenomena. As a measure of average changes, they are very useful in foresting future trends. With the help of index numbers of price, demand, wages, income, etc. a business executive is in a better position to take decision about whether a new product should be launched or whether there is scope for exploring new markets or whether the existing pricing and production policies need a change. Also, it helps in measuring the purchasing power of money and index number are very helpful in deflating national income on the basis of a constant process to enable us to find out whether there is any change in the real income of the people.
You may also like: Index Number

Leave a Reply