2015 Fall Business Mathematics
This is the question set along with answers of 2015 Fall Business Mathematics, which was taken by Pokhara University.
POKHARA UNIVERSITY
2015 Fall Business Mathematics
| Level: Bachelor | Semester – Fall | Year: 2015 |
| Programme: BBA/BBA-BI/ BBA-TT/BCIS/BHCM | Full Marks: 100 | |
| Course: Business Mathematics | Pass Marks: 45 | |
| Time:3hrs | ||
| Candidates are required to give their answers in their own words as far as practicable. | ||
| The figures in the margin indicate full marks. | ||
Section “A”
Very Short Answer Questions
| Attempt all the questions. | 10×2 | |
| 1 | Evaluate: |
2 |
| 2 | Find the interval on which the function |
2 |
| 3 | Determine the function |
2 |
| 4 | Find |
2 |
| 5 | For f(x, y, z) = xeyz find |
2 |
| 6 | Find the elasticity of the demand function q at the given price level p = 3 for q = |
2 |
| 7 | If u = f(x, y) = x2y2 + XY is the utility function for first product x and second product y. Find the marginal utility of second product y. | 2 |
| 8 | A marginal revenue function is given by MR = 800 – 4x. Find the total revenue function if the revenue of 2 items is 2000. | 2 |
| 9 | Find the function with the following property: f’(x) =
|
2 |
| 10 | Draw a graph of the inequality: 2x + 3y |
2 |
Section “B”
Descriptive Answer Questions
| Attempt any six questions | 6×10 | |
| 11 | a) Evaluate: 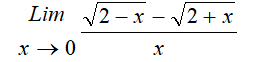 . .
b) A function g(x) is defined by g(x) = Find the value of k so that the function g(x) is continuous at x = 3 |
|
| 12 | a) A product with a large advertising budget has its sales are given by S = 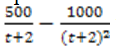 where t is the number of months the product has been on the market. where t is the number of months the product has been on the market.
i. Find the rate of change of sales at any time t. ii. What is the rate of change of sales at t=2? b) The demand function for a firm’s product is q = 150,000 – 75p where q equals the number of units demanded and p equals the price in dollars. i. Determine the price which should be charged to maximize the total revenue. ii. What is the maximum value for total revenue?
|
|
| 13 | a) Determine the locations and values of the absolute maximum for the function Prove that nd = where AR is average revenue and MR is the marginal revenue. |
|
| 14 | a) If U= x2y + y2z + z2x, then prove that 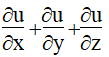 = (x + y + z)2. = (x + y + z)2.
b) A manufacturer of two different types of drugs determines that its monthly revenues from the sale of x units of drug A and y units of drug B are given by i. Find the rate at which revenues will increase with respect to the increase in sales of drug A at x = 4 units and y = 9 units. ii. Find the rate at which revenues will increase with respect to the increase in sales of drug B at x = 4 units and y = 9 units.
|
|
| 15 | a) A sewing machine manufacturer sells its machine in two markets, foreign and domestic. It determines that the profit resulting from the sale of x machines in the domestic and y machines in the foreign market per week is b) Find x and y that maximize the utility function U = x2y2 subject to the budget construction 2x + 4y = 40.
|
|
| 16 | Integrate any two of the following:
a) |
|
| 17 | a) Find the general and particular solution of the differential equation: The demand function for a commodity is and the supply function is, find the consumer’s surplus at the equilibrium market price. |
Section “C”
| Case Analysis | |||||||||||
| 18 | Read the case situation below and answer the questions that follow.
Retailers often sell different brands of competing products. Depending on the joint demand for the products, the retailer may be able to set prices that regulate demand and, therefore, influence profits. Suppose HOME-ALL, Inc., a national chain of home improvement retailers, sells two competing brands of interior flat paint, En-Dure 100 and Croyle& James, which the chain purchases for $8 per gallon and $10 per gallon, respectively. HOME-ALL’s research department has determined the following two monthly demand equations for these paints: D = 120 – 40d + 20c and C = 680 + 30d – 40c Where D is hundreds of gallons of En-Dure 100 demanded at $d per gallon and C is hundreds of gallons of Croyle& James demanded at $c per gallon. For what prices should HOME-ALL sell these paints in order to maximize its monthly profit on these items? To answer this question, complete the following. i) Recall that revenue is a product’s selling price per item the number of items sold. With this in mind, formulate HOME-ALL’s total revenue function for the two paints as a function of their prices. ii) Form HOME-ALL’s profit function for the two paints (in terms of their selling prices). iii) Determine the prices of each type of paint that will maximize HOME-ALL’s profit. iv) Write a brief report to management that details your pricing recommendations and justifies them.
|
||||||||||
| 19 |
|
You may also like Pokhara University|| Fall 2015 English|| BBA/BCIS/BHCM
Do follow us on Online notes Nepal

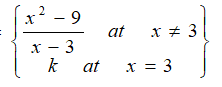
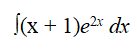 b)
b)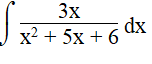 c)
c)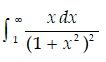
Leave a Reply