
Spring 2016 Business Mathematics
This is the question set along with answers of Spring 2016 Business Mathematics, which was taken by Pokhara University.
POKHARA UNIVERSITY
Spring 2016 Business Mathematics
| Level: Bachelor | Semester – Spring | Year: 2016 |
| Programme: BBA/BBA-BI/BBA-TT/BCIS/ | Full Marks: 100 | |
| Course: Business Mathematics II | Pass Marks: 45 | |
| Time: 3hrs. | ||
| Candidates are required to give their answers in their own words as far as practicable. | |||||||||||||||||||||||||||||||||
| The figures in the margin indicate full marks.
Section “A” Very Short Answer Questions
|
Section “B”
Descriptive Answer Questions
| Attempt any six questions | 6×10 | |
| 11 | a) Evaluate 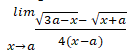
Find the value of K such that the function defined by |
|
| 12 | a) Find the derivative of : b) Sales of pre-paid mobile SIM card are expected to vary with time so that the cumulative sold at t weeks after the sales is launched by i. Find an expression for a weekly rate of change in cumulative sales. Calculate the weekly rate of change in cumulative change sales at |
|
| 13 | a) The total revenue in dollars for a firm is given by R(x) = 8000 -40x2 –x3, where x is the number of units sold per day. Find the number of units that must be sold to maximize revenue. Find the maximum revenue.
Prove that |
|
| 14 | a) A firm estimates that the number of units it sells each year is a function of advertising for TV and radio. The function expressing this relationship is Z = 2000x+5000y -20x2-10y2-50xy where Z is a number of units sold, x is the amount spent on TV advertising and y is the amount spent on radio advertising. The firm is presenting $50000 to TV and $30000 to radio
i. Using partial derivatives, estimate the effect on annual sales if an additional $1000 is allocated to TV. ii. Using partial derivatives, estimate the effect on annual sales if an additional $1000 is allocated to the radio. If v= |
|
| 15 | a) Find the critical point and test their nature for the function b) Examine the relative extreme and test for nature of function f(x, y) =2xy subject to constraint 3x+4y=9. |
|
| 16 | Evaluate (any two)
i. Evaluate: ii. iii. |
|
| 17 | a) find the general and particular solution of the differential equation: Given the demand function pd = 300-x and the supply function ps = x+100, where x is the number of units. Find the consumer’s as well as producer’s surplus, at the level of equilibrium. |
Section “C”
Case Analysis
| Read the scenario and answer the question that follows. | |||||||||||||||||
| 18 | Par, Inc., is a small manufacturer of golf equipment and supplies whose management has decided to move into the market for medium-and high-priced golf bags. Par’s distributor is enthusiastic about the new product line and has agreed to buy all the golf bags par produces will require the following operations.
i. Cutting and dying the material ii. Sewing iii. Finishing (Inserting umbrella hold, clop separators, etc.) iv. Inspection and packaging The director of manufacturing analyzed each of the operations and concluded that if the company produces a medium-priced standard model, each bag will require 7/10 hours in the cutting and dyeing department, ½ hours in the inspection and packaging department. The more expensive deluxe model will require 1 hour for cutting and dyeing 5/6 hours for sewing, 2/3 hours for finishing is summarized in the following table. Par’s production is constrained workload projections, the director of manufacturing estimates that 630 hours for cutting and dyeing 600 hours for sewing, 708 hours for finishing, and 135 hours for inspection and packaging will be available for the production of bags during the next three months.
Production Requirements per Golf Bag
The accounting department analyzed the production data, assigned all relevant variable cost, and arrived at prices for both bags that will result in a profit contribution of $ 10 for every standard bag and $9 for every deluxe bag produced. i. Develop a mathematical model of the par, Inc., a problem that can be used to determine the number of standard bags and the number of deluxe bags to produces in order to maximize total profit contribution. Find an optimum solution |
10 | |||||||||||||||
| 19 | Tire manufacture studying the effectiveness of television advertising and other promotions on sales of its A-brand tires attempted to fit data it had gathered to the equation S = a0 + a1x + a2x2 + b1y where S is sales revenue in millions of dollars, x is millions of dollars spent on television advertising,y is millions of dollars spent on other promotion, and a0, a1, a2, and b1 are constants.
The data, gathered in two different regions of the country where expenditures for other promotions were kept constant (at B1 and B2), resulted in the following equation relating to TV advertising and sales. Region 1: S1 = 30 + 20x – 0.4x2 + B1 Region 2: S2 = 20 + 36x – 1.3x2 + B2 The company wants to know how to make the best use of its advertising dollars in the regions and whether the current allocation could be improved. Advise management about current advertising effectiveness, allocation of additional expenditures, and reallocation of current advertising expenditures by answering the following questions. a) In the analysis of sales and advertising, marginal return to sales is usually used, and it is given by i.Find ii. If $10 million is being spent on TV advertising in each region, what is the marginal return to sales in each region? b) Which region would benefit more from additional advertising expenditure, if $10 million is currently being spent in each region? c) If any additional money is made available for advertising, in which region should it be spent? d) How could money already being spent be reallocated to produce
|
10 |
You may also like Pokhara University||2015 Fall Business Mathematics ||
Do follow us on Online Notes Nepal

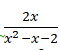 .
.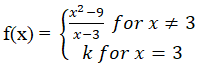 is continuous at x=3.
is continuous at x=3.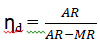 , Where the symbols have their usual meaning.
, Where the symbols have their usual meaning.
Leave a Reply