
Fall 2016 Business Mathematics
This is the question set along with answers of Fall 2016 Business Mathematics, which was taken by Pokhara University.
POKHARA UNIVERSITY
Fall 2016 Business Mathematics
| Level: Bachelor | Semester – Fall | Year: 2016 |
| Program: BCIS | Full Marks: 100 | |
| Course: Mathematics II | Pass Marks: 45 | |
| Time:3hrs | ||
| Candidates are required to give their answers in their own words as far as practicable. | ||
| The figures in the margin indicate full marks. | ||
Section “A”
Very Short Answer Questions
| Attempt all the questions. | 10×2 | |
| 1 | Evaluate 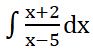 |
2 |
| 2 | Show that |
2 |
| 3 | Test whether the series 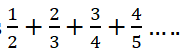 is convergent. is convergent. |
2 |
| 4 | Prove that u = x2 – y2 is harmonic | 2 |
| 5 | Solve the differential equation:
y dx – x dy = x2y dx |
2 |
| 6 | Express in the polar form √ 3 + i | 2 |
| 7 | Integrate |
2 |
| 8 | Define a periodic function with an example. | 2 |
| 9 | Find the period of the function f(x)=cosnx | 2 |
| 10 | Solve |
2 |
Section “B”
Descriptive Answer Questions
| Attempt any six questions | 6×10 | |
| 11 | Integrate any two of the following.
|
|
| 12 | a) Find the volume of solid generated by revolving about the x – axis, the areas bounded by the curve y=5x – x2 and the lines; x = 0, x = 5.
Find the arc length of the curve, y=2/3 (x+1)2/3,0≤x ≤2 |
|
| 13 | Solve the following differential equations:
a) b) |
|
| 14 | a) Solve: Prove that the necessary condition for the convergence of an infinite series ∑un is |
|
| 15 | a) Test for the convergence series of the 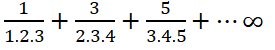
b) Find Fourier sine and cosine integral of the function
|
|
| 16 | a) Find the Fourier series of the function Find the Fourier series of the function |
|
| 17 | Find the harmonic conjugate and corresponding analytic function of What are the necessary conditions for a function of complex variables to be analytic? Show that the function f(z)= |
Section “C”
| Case Analysis | ||
| 18 | a) Let State and prove P-series test. |
You may also like Pokhara University||2015 Fall Business Mathematics ||
Do follow us on Online Notes Nepal

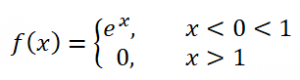
Leave a Reply