Multiple Regression Analysis

Concept of Multiple Regression Analysis:

In simple regression analysis, the regression model is fit between one dependent and one independent variable to estimate the dependent variable or to measure the effectiveness of an independent variable on the dependent variable. When the regression model is fit between one dependent and more the one independent variable then this regression model is called the multiple regression model. In multiple regression analysis, the effect of the different independent variables on the dependent variable can be measured simultaneously.

Let ‘y’ be the dependent variable and x₁, x_2, x₃ …………… x_k be the ‘k’ independent variables. Then the multiple regression model is defined as

Where

y = dependent variable.
x₁, x_2, x₃ …………… x_k  are independent variables.
_β0 = y-intercept.
_β1 = Slope of y with variable x₁ holding the remaining variables x_2, x₃ …,x_k constant or Regression coefficient of y on x₁ holding the remaining variables x_2, x₃ …………… x_k constant.
_β2 = Slope of y with variable x₂ holding the remaining variables x_1, x₃ …,x_k constant or Regression coefficient of y on x₂ holding the remaining variables x_1, x₃ …………… x_k constant.
_β3 = Slope of y with variable x₃ holding the remaining variables x_1, x_2, x_4,  …,x_k constant or Regression coefficient of y on x₃ holding the remaining variables x_1, x_2, x_4,  …,x_k constant.
And so on. Similarly,
_βk = Slope of y with variable x_k holding the remaining variables  x_1, x_2, x₃ …,x_k-1 constant or Regression coefficient of y on x_k holding the remaining variables x_1, x_2, x₃ …,x_k-1 constant.
e = error term or residual.

Multiple Regression Model with Two Independent Variables:

Let ‘y’ be the dependent variable and x₁ and x₂ are two independent variables. The multiple regression model with two independent variables is defined as,

Where

y = dependent variable.
x₁and x₂ are independent variables.
_β0 = y-intercept.
_β1 = Slope of y with variable x₁ holding the remaining variable x₂ constant or Regression coefficient of y on x₁ holding the remaining variable x₂ constant.
_β2 = Slope of y with variable x₂ holding the remaining variable x₁ constant or Regression coefficient of y on x₂ holding the remaining variable x₁ constant.
e = error term or residual.

To fit the regression model (2), we have to estimate the value of _β0, _β1, and _β2. To estimate the value of these parameters we use the principle of lest square. The following three normal equations of equation (2) can be obtained using the method of least square.

Now normal equations of equation (2) are

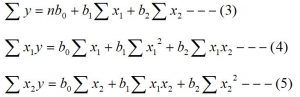
On solving these above three normal equations we can estimate the value of _β0, _β1, and _β2. Hence the fitted multiple regression model is

Where,
The estimated value of the dependent variable for a given value of the independent variables.
_β0 = y-intercept (or Estimated value of _β0.)
b1 = Regression coefficients of y on x1 holding the effect of x2 constant (or Estimated
value of _β1.)
b2 = Regression coefficients of y on x2 holding the effect of x1 constant (or Estimated
value of _β2.)

Interpreting the multiple regression coefficients:

Suppose we have the following multiple regression model

1. The y-intercept _β0 represents the average of the dependent variable when the value of independents variables are zero i.e. x₁ = x₂ =0. for example

Here _β0 = 20, this means, the average value of dependent variable is 20 when x₁ = x₂ =0

2. The multiple regression coefficients b₁ measure the average rate of increased or decreased in the value of a dependent variable (y) while         increasing the value of independent variable ‘x₁’ by unit, by keeping the effect of another independent variable ‘x₂’ constant. For example,

Here, _β1 = 2.5, this means, the value of a dependent variable (y) is increased by 2.5 when the value of an independent variable (x₁) is                 increased by 1, by keeping the effect of x₂ constant.

3. The multiple regression coefficients _β2 measure the average rate of increased or decreased in the value of a dependent variable (y)                     while increasing the value of independent variable ‘x₂’ by unit, by keeping the effect of other independent variables ‘x₁’ constant. For                 example,

Here, _β2 = -3.8, this means, the value of the dependent variable (y) is decreased by 3.8 when the value of an independent variable (x₂) is increased by 1, by keeping the effect of x₁ constant.

Error term or Residual:

The difference between the observed and estimated value of the dependent variable (y) is called error or residual and it is denoted by ‘e’

Where

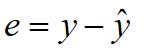
e = Error term

y= Observed value of the dependent variable.

= Estimated value of the dependent variable for a given value of a set of independent variables.

 

You may also like: Confidence Interval Estimate