Karnaugh Map
The Karnaugh map (KM or K-map) is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953 as a refinement of Edward Veitch’s 1952 Veitch chart, which actually was a rediscovery of Allan Marquand’s 1881 logical diagram aka Marquand diagram but with a focus now set on its utility for switching circuits. Veitch charts are therefore also known as Marquand–Veitch diagrams, and Karnaugh maps as Karnaugh–Veitch maps (KV maps).
Minimization by K-map
Algebraic minimization of Boolean functions is rather awkward because it lacks specific rules to predict each succeeding step in the manipulative process. The map method provides a simple straightforward procedure for minimizing Boolean functions. This method may be regarded as a pictorial form of a truth table. The map method, first proposed by Veitch and modified by Karnaugh, is also known as the “Veitch diagram” or the “Karnaugh map.”
i. The k-map is a diagram made up of a grid of squares.
ii. Each square represents one minterm.
iii. The minterms are ordered according to Gray code (only one variable changes between adjacent squares).
iv. Squares on edges are considered adjacent to squares on opposite edges.
v. Karnaugh maps become clumsier to use with more than 4 variables.
In fact, the map presents a visual diagram of all possible ways a function may be expressed in a standard form. By recognizing various patterns, the user can derive alternative algebraic expressions for the same function, from which he can select the simplest one. We shall assume that the simplest algebraic expression is anyone in a sum of products or product of sums that has a minimum number of literals.
(This expression is not necessarily unique)
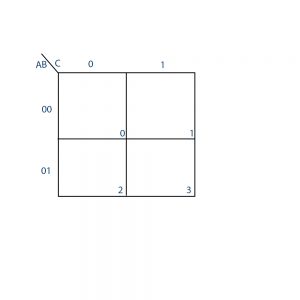
Two variable maps
There are four minterms for a Boolean function with two variables. Hence, the two-variable map consists of four squares, one for each minterm, as shown in Figure:
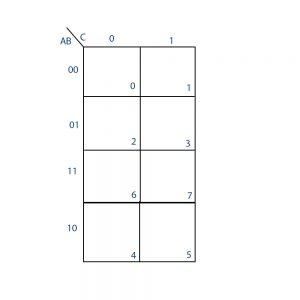
Three variable maps
There are eight minterms for three binary variables. Therefore, a three-variable map consists of eight squares, as shown in Figure. The map was drawn in part (b) is marked with binary numbers for each row and each column to show the binary values of the minterms.
Four variable maps
The map for Boolean functions of four binary variables is shown in Fig below. In (a) are listed the 16 minterms and the squares assigned to each. In (b) the map is redrawn to show the relationship with the four variables.
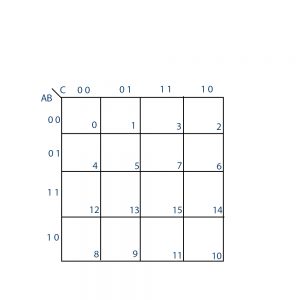
The map minimization of four-variable Boolean functions is similar to the method used to minimize three-variable functions. Adjacent squares are defined to be squares next to each other. In addition, the map is considered to lie on a surface with the top and bottom edges, as well as the right and left edges, touching each other to form adjacent squares. For example, m0 and m2 form adjacent squares, as do m3
and m11.
Don’t care Conditions
The logical sum of the minterms associated with a Boolean function specifies the conditions under which the function is equal to 1. The function is equal to 0 for the rest of the minterms. This assumes that all the combinations of the values for the variables of the function are valid. In practice, there are some applications where the function is not specified for certain combinations of the variables.
For example a four-bit binary code for the decimal digits has six combinations that are not used and consequently, are considered as unspecified.
In most applications, we simply don’t care what value is assumed by the function of the unspecified minterms. For this reason, it is customary to call the unspecified minterms of a function don’t-care conditions. These don’t-care conditions can be used on a map to provide further simplification of the Boolean expression.
Don’t-care minterm is a combination of variables whose logical value is not specified. To distinguish the don’t-care condition from 1’s and 0’s, and X is used. Thus, an X inside a square in the map indicates that we don’t care whether the value of 0 or 1 is assigned to F for the particular minterm. When choosing adjacent squares to simplify the function in a map, the don’t-care minterms may be assumed to be either 0 or 1. When simplifying the function, we can choose to include each don’t-care minterm with either the 1’s or the 0’s, depending on which combination gives the simplest expression.
Product of sum simplification
The optimized Boolean functions derived from the maps in all of the previous examples were expressed in sum-of-products (SOP) form. With only minor modification, the product-of-sums form can be obtained.
Procedure:
The 1’s placed in the squares of the map represent the minterms of the function. The minterms not included in the function belonging to the complement of the function. From this, we see that the complement of a function is represented in the map by the squares not marked by 1’s. If we mark the empty squares with 0’s and combine them into valid rectangles, we obtain an optimized expression of the complement of the function (F’). We then take the complement of F to obtain the function F as a product of sums.
Question: Simplify the following Boolean function (, , ,) = (0, 1, 2, 5, 8, 9, 10) in
(a) Sum of products (SOP) and
(b) Product of sums (POS).
Solution:
The 1’s marked on the map below represent all the minterms of the function. The squares marked with 0’s represent the minterms not included in F and, therefore, denote F’.
(a) Combining the squares with 1’s gives the simplified function in sum of products:
F = B’D’ + B’C’ + A’C’D
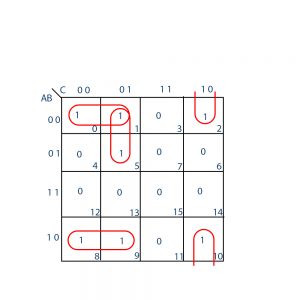
(b) If the squares marked with 0’s are combined, as shown in the diagram, we obtain the simplified complemented function:
F’ = AB + CD + BD’
Applying DeMorgan’s theorem (by taking the dual and complementing each literal as described, we obtain the simplified function in a product of sums:
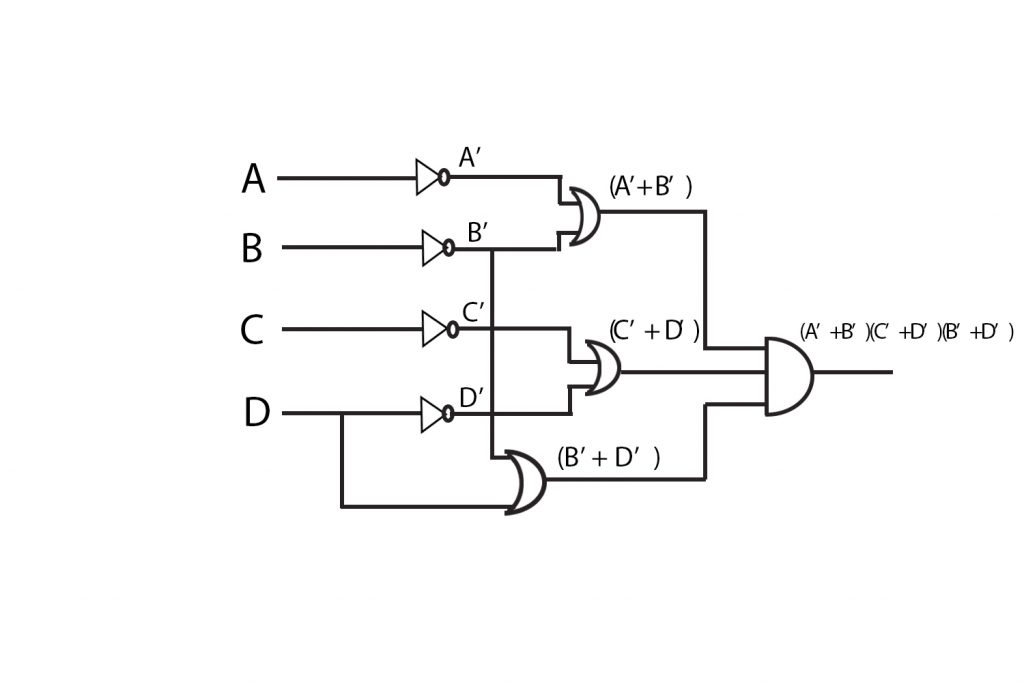
F = (A’ + B’)(C’ + D’)(B’ + D)
The Gate implementation of the simplified expressions obtained above in (a) and (b):
You may also like combinational circuit

Leave a Reply