
Median Data
The variable values dividing the total set of observations into two equal parts of the data is called the median data.
For a data set, it may be thought of as the “middle” value.
For example, in the data set [1,3,3,6,7,8,9], the median is 6, the fourth largest, and also the fourth smallest, number in the sample.
For Individual Series
- First, we change the data in ascending or descending order of their magnitude.
- If the number of observations is odd, then the middle value gives the median among all the data.
- Again, if the number of observations is even then there will be two middle values, the average of two middle values gives the median.
- The formula for computing the median in case of individual series is given by
![]()
where,
n=Number of Observations
For discrete series,
- Arrange the data in ascending order of their magnitude.
- From the cumulation frequency table.
- Find the value of
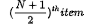 .
. - See the cumulation frequency table equal to or just greater than
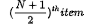 .
. - Note the corresponding value of x which gives the value of the median.
where,
N=Number of Observations
For Continuous Series,
- Prepare a c.f. table.
- Find
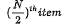
- See if the value in c.f. the table is equal to or greater than
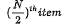 , note the class.
, note the class. - The corresponding class contains the value of the median and is called the median class.
- The following formula is used in finding the median:
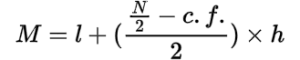
where
l=lower limit of the median class
f=frequency of the median class
c.f.=c.f. of preceding median class
h=size of the median class
You may also like Arithmetic Mean

Leave a Reply