
Arithmetic Mean
A simple mean of a set of observations is the sum of all observations divided by the number of observations. The arithmetic mean is used frequently in many diverse fields such as economics, anthropology, and history, and it is used in almost every academic field to some extent.
For Individual Series,
Let x1, x2, … , xn be the ‘N’ number of observations then mean is denoted by ![]()
Direct Method
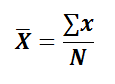 Short-cut Method
Short-cut Method
where, d = X-A A = Assumed Mean
For Discrete Series,
Let x1, x2, … , xn be the ‘N’ number of observations with their respective frequencies f1, f2, … , fn then their mean is denoted by X and is given by:
Direct Method
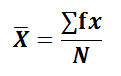
Shortcut Method
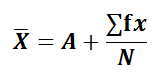
For Continuous Series,
The formula for calculating the value of arithmetic mean in continuous series is the same as in the case of discrete series only the difference is that ‘x’ be the mid-value of the corresponding class in corresponding class in continuous series.
Direct Method
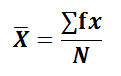
Shortcut Method
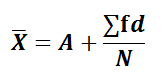
Step-deviation Method
Properties of Arithmetic Mean
1. The solution to the deviation of the items taken from their arithmetic mean is zero.
ie. 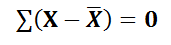
2. The sum of the square of deviation of the items taken from their arithmetic mean is minimum.
ie. ![]()
3. Let X1 be the mean of ‘n1’ number of observations and X2 be the mean of ‘n2’ number of observations than their combined mean is denoted by X12 and is given by:
ie. ![]()
Weighted Mean
Let W1, W2, …, Wn be the weight to the variant values X1, X2, …, Xn then their weighted mean is denoted by ![]()
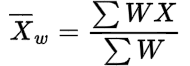
You may also like: Range, Quartile Deviation, and Standard Deviation || Measures of Dispersion

Leave a Reply