Types of Number System || Number System || Bcis Notes

NUMBER SYSTEM

Number systems are the technique to represent numbers in the computer system architecture, every value that you are saving or getting into/from computer memory has a defined number system.

When we type some letters or words, the computer translates them in numbers as computers can understand only numbers. A computer can understand the positional number system where there are only a few symbols called digits and these symbols represent different values depending on the position they occupy in the number.

NOTES-

The value of each digit in a number can be determined using −

• The digit
• The position of the digit in the number
• The base of the number system (where the base is defined as the total number of digits available in the number system)

TYPES OF NUMBER SYSTEM

The types of Number System are as follows:-

• Binary number system
• Octal number system
• Decimal number system
• Hexadecimal (hex) number system,

 

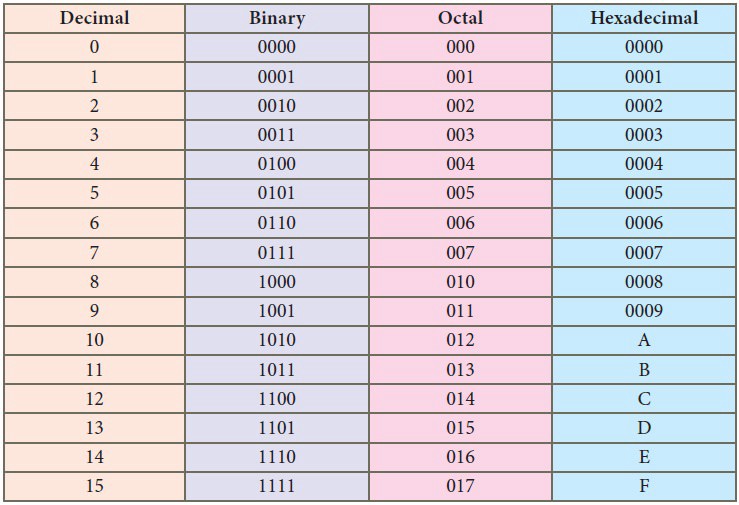
1. Binary Number System

The binary number system is a numbering system that represents numeric values using two unique digits (0 and 1). Most computing devices use binary numbering to represent the electronic circuit voltage state, (i.e., on/off switch), which considers 0 voltage input as off and 1 input as on.

Characteristics of the binary number system are as follows −

• Uses two digits, 0 and 1
• Also called a base 2 number system
• Each position in a binary number represents a 0 power of the base (2). Example 2⁰
• The Last position in a binary number represents an x power of the base (2). Example 2^x where x represents the last position – 1.

Example-(10101)₂, (1010100)₂

2. Decimal Number System

The word ‘deci’ means 10, therefore there are ten numbers (digits) in the decimal number system. The valid numbers in a base 10 number system are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Characteristics of the Decimal Number system are as follows −

• Uses 10 digits, i.e. 0 to 9
• Also called a base 10 number system
• Each position represents a specific power of the base (10).
• In the decimal number system, the successive positions to the left of the decimal point represent units, tens, hundreds, thousands, and so on.

Example– (686)₁₀, (789)₁₀

3. Octal Number system

The number system whose base is 8 is known as the octal number system. The base 8 means the system uses eight digits from 0 to 7. All the eight digits from 0 to 8 have the same physical meaning as that of decimal numbers.

Characteristics of the octal number system are as follows −

• Uses eight digits, 0,1,2,3,4,5,6,7
• Also called a base 8 number system
• Each position in an octal number represents a 0 power of the base (8). Example 80
• The Last position in an octal number represents an x power of the base (8). Example 8x where x represents the last position – 1

Example– (246)₈, (456)₈

4. Hexadecimal Number System

Hexadecimal describes a base-16 number system. That is, it describes a numbering system containing 16 sequential numbers as base units (including 0) before adding a new position for the next number. (Note that we’re using “16” here as a decimal number to explain a number that would be “10” in hexadecimal.) The hexadecimal numbers are 0-9 and then use the letters A-F.

Characteristics of the hexadecimal number system are as follows −

• Uses 10 digits and 6 letters, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• Letters represent the numbers starting from 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15
• Also called a base 16 number system
• Each position in a hexadecimal number represents a 0 power of the base (16). Example, 16⁰
• The Last position in a hexadecimal number represents an x power of the base (16).   Example 16^x where x represents the last position – 1.

Example– (DE100)₁₆ , (1ABC)₁₆

 

Table of Number system-

 

you may also like the binary codes      arithmetic operation of number-system