
Binary Codes are described below:-
- Gray Binary Codes
- Alphanumeric Binary Codes
- ASCII Binary Codes
- EBCDIC Binary Codes
- BCD Binary Codes
a. Gray Code (Reflected code)
Gray Code system is a binary code in which every successive pair of numbers differs in only one bit. It is used in applications in which the normal sequence of binary numbers generated by the hardware may produce an error or ambiguity during the transition from one number to the next.
Gray Code is one of the most important codes. It is a non-weighted code that belongs to a class of codes called minimum change codes. In these codes, while traversing from one step to another step only one bit in the code group changes. In the case of Gray Code two adjacent code numbers differ from each other by only one bit.
The idea of it can be cleared from the table given below.
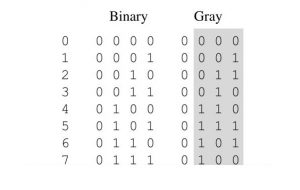
From this table, we can obtain the equivalent gray code of the decimal numbers. There are several steps which will make you understand how the codes are formed. (1) In the case of gray-code, one bit will change from its previous in each step. One thing must be kept in mind that the change of bit always occurs from the right side i.e from L.S.B towards the M.S.B. At first, the first three bits are constant I,e 000 and the fourth-bit changes from 0 to 1. We know that for binary digit possible combination is 0 and 1, so keeping first three-bit constant the possible combination of a 4th bit is over for decimal 0 and 1 respectively.
Use of Gray codes:
- Gray codes are used in rotary and optical encoders, Karnaugh maps, and error detection.
b. Alphanumeric Code:
The Alphanumeric character set is a set of elements that includes the 10 decimal digits, 26 letters of the alphabet, and special characters such as $, %, +, etc. It is necessary to formulate a binary code for this set to handle different data types. If only capital letters are included, we need a binary code of at least six bits, and if both uppercase letters and lowercase letters are included, we need a binary code of at least seven bits.
c. ASCII character code
The standard binary code for the alphanumeric characters is called ASCII (American Standard Code for Information Interchange). It uses seven bits to code 128 characters as shown in the table below. The seven bits of the code are designated by B1 through B7 with B7 being the most significant bit.
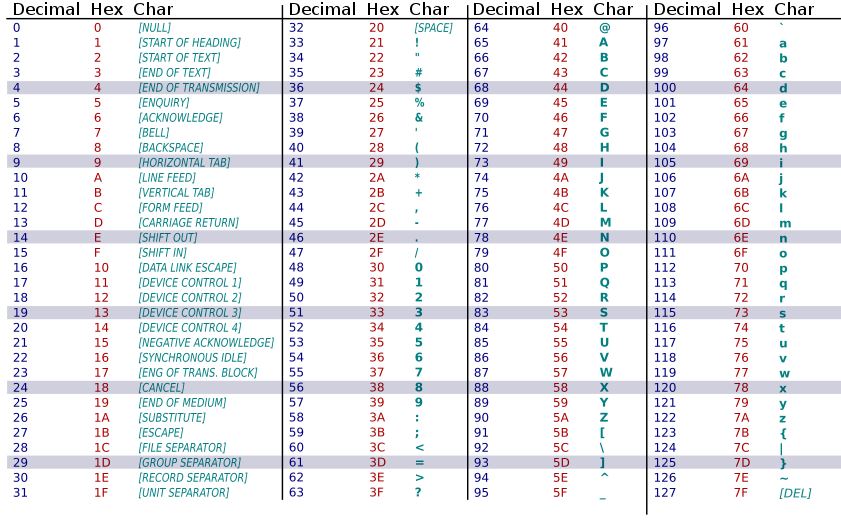
Example:
ASCII for each symbol is (B7B6B5B4B3B2B1)
G ← 100 0111, ( ← 010 1000, h ← 110 1000, > ← 011 1110 and so on.
d. EBCDIC character code:
EBCDIC (Extended Binary Coded Decimal Interchange Code) is another alphanumeric code used in IBM equipment. It uses eight bits for each character. EBCDIC has the same character symbols as ASCII, but the bit assignment for characters is different. As the name implies, the binary code for the letters and numerals is an extension of the binary-coded decimal (BCD) code. This means that the last four bits of the code range from 0000 through 1001 as in BCD.
e. BCD code
In this code, each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in the BCD code only the first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.
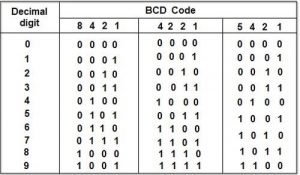
Advantages of BCD Codes
- It is very similar to the decimal system.
- We need to remember the binary equivalent of decimal numbers 0 to 9 only.
Disadvantages of BCD Codes
- The addition and subtraction of BCD have different rules.
- The BCD arithmetic is a little more complicated.
- BCD needs the number of bits than binary to represent the decimal number. So BCD is less efficient than binary.
you may also like the binary system

Leave a Reply