
This is the question set along with answers of Mathematics – I – Spring, 2016, which was taken by the Pokhara University.
Pokhara University – Mathematics, Spring 2016
| Level: Bachelor | Semester – Spring | Year: 2016 |
| Program: BCIS | Full Marks: 100 | |
| Course: Mathematics – I, Spring 2016 | Pass Marks: 45 | |
| Time: 3hrs. | ||
| Candidates are required to give their answers in their own words as far as practicable. |
| The figures in the margin indicate full marks. |
| Section “A”
Very Short Answer Questions Attempt all the questions. |
10×2 |
|
| 1. | If U = {4, 5, 6, 7, 8, 9, 10}, P = {6, 7, 8, 9} and Q = {5, 7, 9}, Find the
elements of the set P’-Q’ . |
|
| 2. | Rewrite < 7 without using the absolute value sign. | |
| 3. | Sketch the graph of the function f(x) = . | |
| 4. | Find a 2 ´ 2 matrix A = [ a ij ] where a ij = i – 2 j | |
| 5. | If, show that = O, where I and O are identity and null matrixes of order 2. | |
| 6. | Is the function f(x) = 3x3 – 4x – 2 increasing or decreasing at x = 1 ? | |
| 7. | In how many ways can a student choose 5 questions out of 10 questions,
if 2 questions are compulsory? |
|
| 8. | Show that the vectors 2 +2 – and 2 -3 -2 are at the right angle. | |
| 9. | Determine.
|
|
| 10. | Find the derivative of y = x2.logx.
|
|
| Section “B”
Descriptive Answer Questions Attempt any six questions |
6×10 | |
| 11. | a) In a group of students 30 read Mathematics, 24 read Economics, 22 read Statistics, 14 read mathematics only, 8 read Economics only, 6 read Mathematics and Statistics only, 2 read Mathematics and Economics only and 8 read none of these subjects.
i) How many students are there in the group? ii) How many read Economics and Statistics only? iii) How many read Statistics only? iv) How many read all three subjects? b) Find the domain and range of y = |
|
| 12. | a) Determine the value of the constant K so that the function
is continuous at x = 1. b) If and, find. |
|
| 13. | a) If A = [1, 3) and B = (2, 5], find A∪ B, A∩ B and A – B, B –A.
b) Let A = {1, 2, 3, 4}. Find a relation on A × A determined by the condition x + y< 5. |
|
| 14. | a) An epidemic is spreading through a large western region. Health officials estimate that the number of persons who will be affected by the diseases is a function of time since the diseases were first detected.
Specifically, the function is, where n is the number of people and, measured in days. i. How many persons are expected to have caught the disease after 20 days?. ii. At what rate is the disease spreading at t = 30? b) Determine the values of the absolute maximum and minimum for the function in the interval [-2, 5].
|
|
| 15. | a) Suppose that the total cost in dollars of manufacturing q units of a certain commodity is.
i) Find the average cost function. ii) Find the marginal cost function. b) Check whether the following set of vectors is linearly dependent or independent. (3, 1, -4), (2, -1, 3) and (1, 0, 1). |
|
| 16. | a) A student is required to answer 8 out of 12 questions which are divided into 2 groups each containing 6 questions, and that student is not permitted to attempt more than 5 from any group. In how many different ways can the student make up choice?
b) Find the derivatives of the following (any two) i) ii) (3x2 + 7x + 1)5 iii) e2x. log (5x + 1) |
|
| 17. | a) Prove that
b) Solve the following system of equations by using Cramer’s rule or matrix method. x + 2y – z = -5, 2x – y + z = 6 and x- y – 3z = -3 |
|
| 18. | Section “C”
Attempt all questions A manufacturer of the cycle has a fixed cost of $500. The producer experiences a variable cost of $30 per cycle. Suppose the manufacturer of the cycle can sell its products for $80 each. a) Find the total cost function at a production level of x cycles. b) Find the revenue function R associated with output level x. c) Determine the manufacturer’s profit function P. d) How many cycles should be produced in order to have a break- even? e) Suppose that the manufacturer produces 15 cycles. What corresponding profit should the manufacturer get?
|
2×10 |
| 19. | Sales of a Pre – Paid mobile SIM cards are expected to vary with time so
that the cumulative total sold at t weeks after the sales is launched by NTC, S(t), given by the following equation; S(t) = Find an expression for the weekly rate of change in cumulative sales. Calculate the weekly rate of change in cumulative sales at the end of 30th weeks. |
|
You may also like Pokhara University || Fall,2014 || Introductory Microeconomics || BBA\BCIS

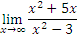
Leave a Reply